ARTIQ (Advanced Real-Time Infrastructure for Quantum physics) is a leading-edge control system for quantum information experiments. It was initiated and developed in partnership with the Ion Storage Group at NIST, and is now used and supported by a growing number of research institutions worldwide. While ARTIQ is currently mostly used by atomic physics groups, its applicability reaches beyond ion trapping.


Modern research on quantum information systems poses particular challenges to the control system:
- dozens of signals need to be received and generated with extremely precise timing, in particular to ensure phase coherence
- quantum error correction schemes require very low reaction latency in response to a measurement
- real-world implementations of quantum gates, and a fortiori quantum algorithms, involve structurally complex protocols
- ever-improving experimental techniques drive the need for a flexible and programmable system
- the diversity of equipment, device drivers and data analysis software involved in a single experiment results in a distributed and multi-platform environment
Enter ARTIQ
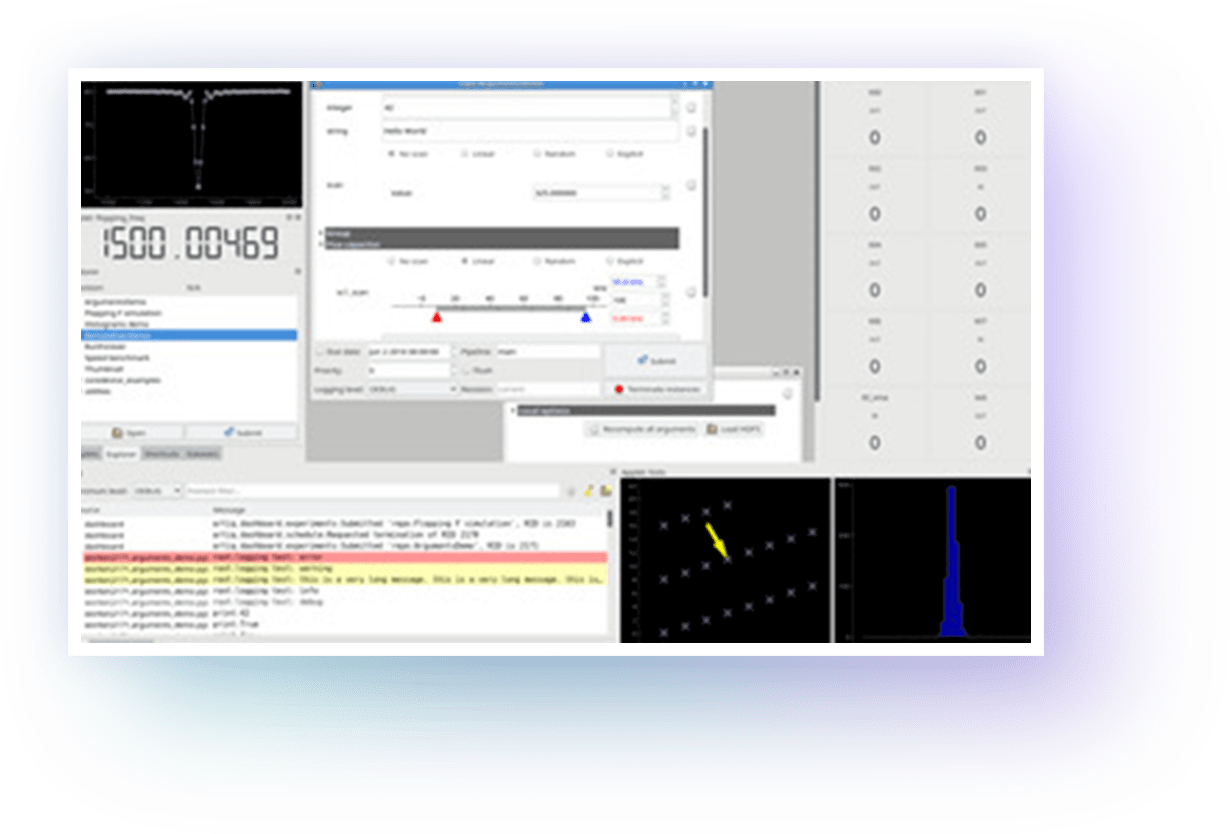
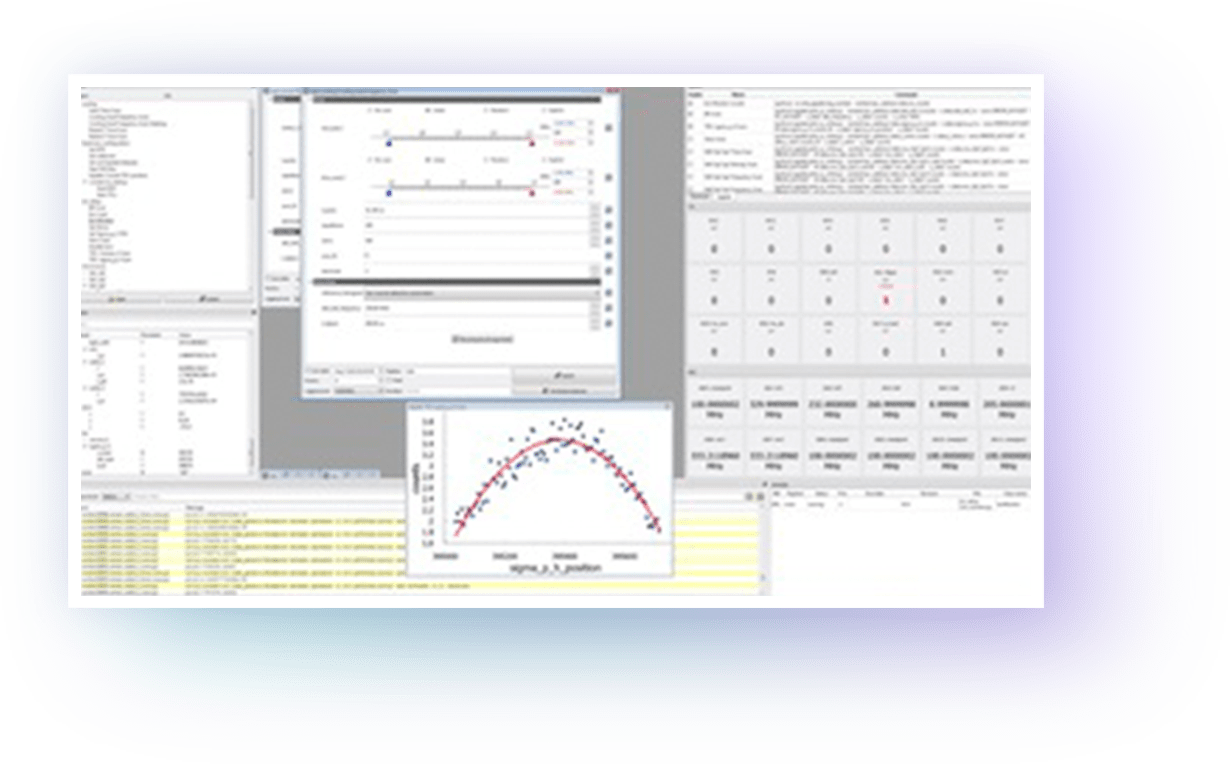
ARTIQ features a high-level programming language, based on Python, that helps describing complex experiments. It is compiled and executed on dedicated FPGA hardware with nanosecond timing resolution and sub-microsecond latency.
The time-critical code (a kernel) running on the FPGA (the core device) is easily interfaced with Python code on the computer using a remote procedure call (RPC) mechanism.
The FPGA design is highly portable so that it can adapt to different laboratory setups and resist hardware obsolescence.
ARTIQ drivers for non-realtime devices can be run on remote machines with different operating systems.
The project also includes a graphical user interface, an experiment scheduling system, and databases for experiments, devices, parameters and results.
Technologies employed include Python, Migen, MiSoC/mor1kx, LLVM and llvmlite.

Ecosystem

ARTIQ was initiated by the Ion Storage Group at NIST, and other partners have contributed to major features and developments related to ARTIQ and/or Sinara. See Funding and licensing model for more details.
Open source
Another goal of ARTIQ is to streamline and simplify the design flow of quantum physics instrumentation by promoting design reuse through the development of platform-independent, open-source hardware and software.
Our aim is to provide a control system suitable for the challenges of modern quantum information research, which is based on modular, parameterized and open components that allow physicists to rapidly design and deploy new experiments.

Sinara hardware
The first ARTIQ core devices used hardware built in-house by physicists. To improve the quality, features and scalability of ARTIQ systems, we have been developing the Sinara device family. It provides turnkey control hardware that is reproducible, open, flexible, modular, well-tested, and well-supported by the ARTIQ control software.
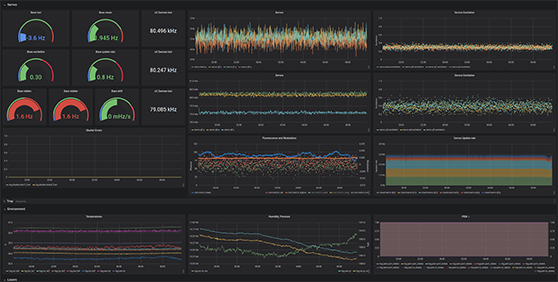
Grafana linked to ARTIQ, monitoring an Opticlock ion trap